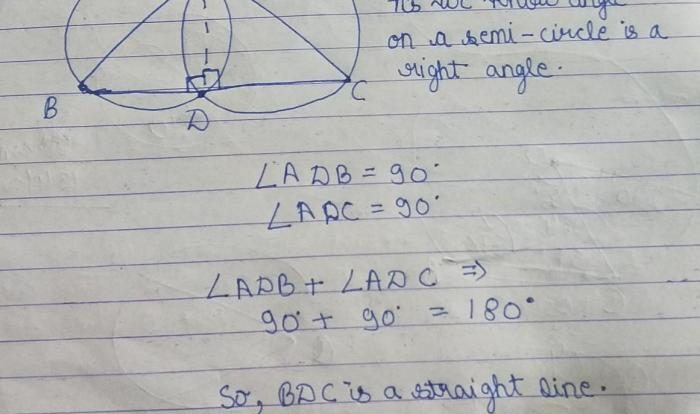Unit 8 polygons and quadrilaterals homework 1 angles of polygons – Embark on an enlightening journey through Unit 8: Polygons and Quadrilaterals Homework 1, where we delve into the captivating realm of polygon angles. Prepare to unravel the intricacies of vertices, edges, and sides, unlocking the mysteries that govern the geometry of these fascinating shapes.
As we progress, we will explore the diverse world of quadrilaterals, delving into the unique characteristics of squares, rectangles, parallelograms, and trapezoids. Along the way, we will unravel the secrets of interior and exterior angles, uncovering the profound relationship between the number of sides and the sum of interior angles.
Polygon Basics
A polygon is a closed figure in a plane bounded by three or more straight line segments. The line segments are called sides, and the points where the sides intersect are called vertices.
Polygons are classified based on the number of sides they have. A triangle has three sides, a quadrilateral has four sides, a pentagon has five sides, and so on.
Types of Polygons
- Convex polygon: A polygon is convex if all of its interior angles are less than 180 degrees.
- Concave polygon: A polygon is concave if it has at least one interior angle that is greater than 180 degrees.
- Regular polygon: A polygon is regular if all of its sides are equal in length and all of its interior angles are equal in measure.
- Irregular polygon: A polygon is irregular if it is not regular.
Quadrilaterals
A quadrilateral is a polygon with four sides. There are many different types of quadrilaterals, including squares, rectangles, parallelograms, and trapezoids.
Types of Quadrilaterals
- Square: A square is a regular quadrilateral with four equal sides and four right angles.
- Rectangle: A rectangle is a quadrilateral with four right angles and two pairs of parallel sides.
- Parallelogram: A parallelogram is a quadrilateral with two pairs of parallel sides.
- Trapezoid: A trapezoid is a quadrilateral with one pair of parallel sides.
Angles of Polygons
The interior angle of a polygon is the angle formed by two adjacent sides of the polygon. The exterior angle of a polygon is the angle formed by one side of the polygon and the extension of the adjacent side.
Sum of Interior Angles of a Polygon
The sum of the interior angles of a polygon with nsides is given by the formula:
(n
2) × 180°
Angle Properties of Quadrilaterals
The angle properties of quadrilaterals depend on the type of quadrilateral.
Angle Properties of Squares and Rectangles
- All interior angles are right angles (90°).
- Opposite angles are equal.
- Adjacent angles are supplementary (add up to 180°).
Angle Properties of Parallelograms
- Opposite angles are equal.
- Adjacent angles are supplementary (add up to 180°).
Angle Properties of Trapezoids
- Opposite angles are supplementary (add up to 180°).
Applications of Polygon Angle Properties: Unit 8 Polygons And Quadrilaterals Homework 1 Angles Of Polygons
Polygon angle properties are used in a variety of applications, including architecture, engineering, and design.
Architecture, Unit 8 polygons and quadrilaterals homework 1 angles of polygons
- Determining the angles of a roof.
- Designing the layout of a building.
Engineering
- Calculating the forces on a bridge.
- Designing the shape of a car.
Design
- Creating patterns for clothing and textiles.
- Designing logos and other graphics.
Key Questions Answered
What is a polygon?
A polygon is a closed plane figure with three or more straight sides.
What is the difference between a polygon and a quadrilateral?
A quadrilateral is a polygon with four sides, while a polygon can have any number of sides.
What is the formula for the sum of interior angles of a polygon?
(n-2) x 180 degrees, where n is the number of sides.