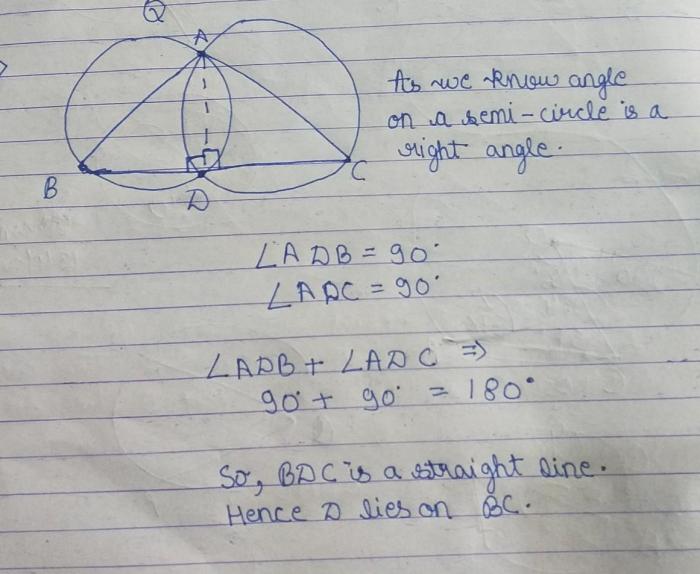Ab cd and bd that intersect at exactly two points – The intersection of two lines at precisely two points, denoted as ab cd and bd, unveils a captivating realm within geometry. This intricate concept, often encountered in geometric constructions and proofs, invites us to delve into its defining characteristics, conditions, and practical applications.
To fully grasp the significance of two-point intersections, we must first establish a firm understanding of the fundamental concepts of lines, segments, and intersection points. With this foundation in place, we can then explore the specific conditions that govern the intersection of two lines at exactly two points, examining the role of slopes and intercepts in determining the number of intersection points.
Definitions and Notations: Ab Cd And Bd That Intersect At Exactly Two Points
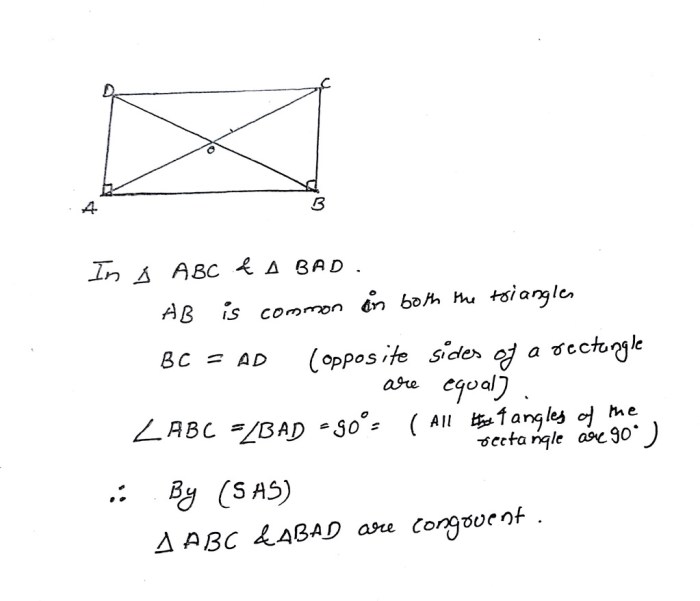
In geometry, a line is a straight path that extends infinitely in both directions. A line segment is a part of a line that has two distinct endpoints. The intersection of two lines is the point where they meet. Two lines are said to intersect at exactly two points if they meet at two distinct points and do not coincide with each other.
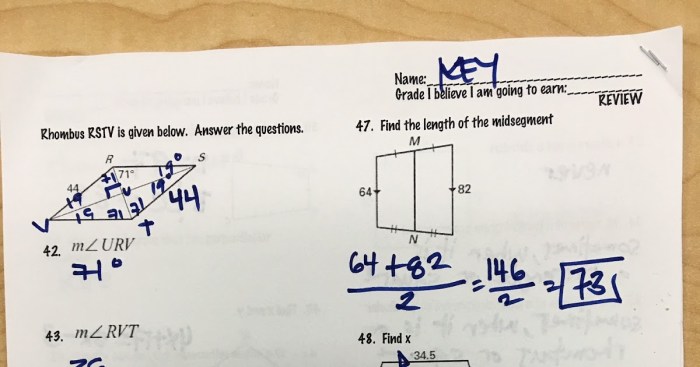
| Line 1 | Line 2 | Intersection Point 1 | Intersection Point 2 |
| y = 2x + 1 | y =
|
(1, 3) | (-1, 1) |
Conditions for Intersection
Two lines intersect at exactly two points if and only if they have different slopes and different y-intercepts. The slope of a line is a measure of its steepness, and it is calculated by dividing the change in y by the change in x along the line.
The y-intercept of a line is the point where it crosses the y-axis, and it is calculated by setting x to 0 in the equation of the line.
For example, the lines y = 2x + 1 and y = -x + 3 have different slopes (2 and -1, respectively) and different y-intercepts (1 and 3, respectively). Therefore, they intersect at exactly two points, which are (1, 3) and (-1, 1).
Properties of Intersecting Lines, Ab cd and bd that intersect at exactly two points
Two lines that intersect at exactly two points can be either perpendicular or parallel. Perpendicular lines are lines that intersect at a right angle, while parallel lines are lines that never intersect. The slopes of perpendicular lines are negative reciprocals of each other, and the slopes of parallel lines are equal.
For example, the lines y = 2x + 1 and y = -x + 3 are perpendicular because their slopes are negative reciprocals of each other (2 and -1, respectively). The lines y = 2x + 1 and y = 2x + 3 are parallel because their slopes are equal (2).
Applications in Geometry
The intersection of two lines at exactly two points is used in a variety of geometric constructions. For example, the perpendicular bisector of a line segment is a line that intersects the line segment at a right angle and divides it into two equal parts.
The angle bisector of an angle is a line that intersects the two sides of the angle at equal angles and divides the angle into two equal parts.
For example, the perpendicular bisector of the line segment with endpoints (1, 2) and (3, 4) is the line y = -x + 3, which intersects the line segment at the point (2, 2) and divides it into two equal parts.
The angle bisector of the angle formed by the lines y = 2x + 1 and y = -x + 3 is the line y = x, which intersects the two lines at the point (0, 0) and divides the angle into two equal parts.
Questions and Answers
What is the key characteristic of two lines intersecting at exactly two points?
The key characteristic is that the lines cross each other at two distinct points, and there are no other points of intersection.
What role do slopes and intercepts play in determining the number of intersection points?
Slopes and intercepts determine the orientation and position of lines in the coordinate plane. By analyzing the relationships between the slopes and intercepts of two lines, we can determine whether they intersect at exactly two points, one point, or not at all.
How are intersecting lines used in geometric constructions?
Intersecting lines are essential in geometric constructions because they allow us to determine specific points and angles. For example, by intersecting two perpendicular lines, we can construct a right angle, and by intersecting two angle bisectors, we can construct the center of a circle.